This function will fit a linear model to two variables. The criterion can be continuous or binary. For logistic regression, set family = 'binomial'. For poisson regression, set family = 'poisson'. If omitted, family will default to 'gaussian' for standard linear regression.
biVarPlot(data, x, y, family = "Gaussian")Arguments
Examples
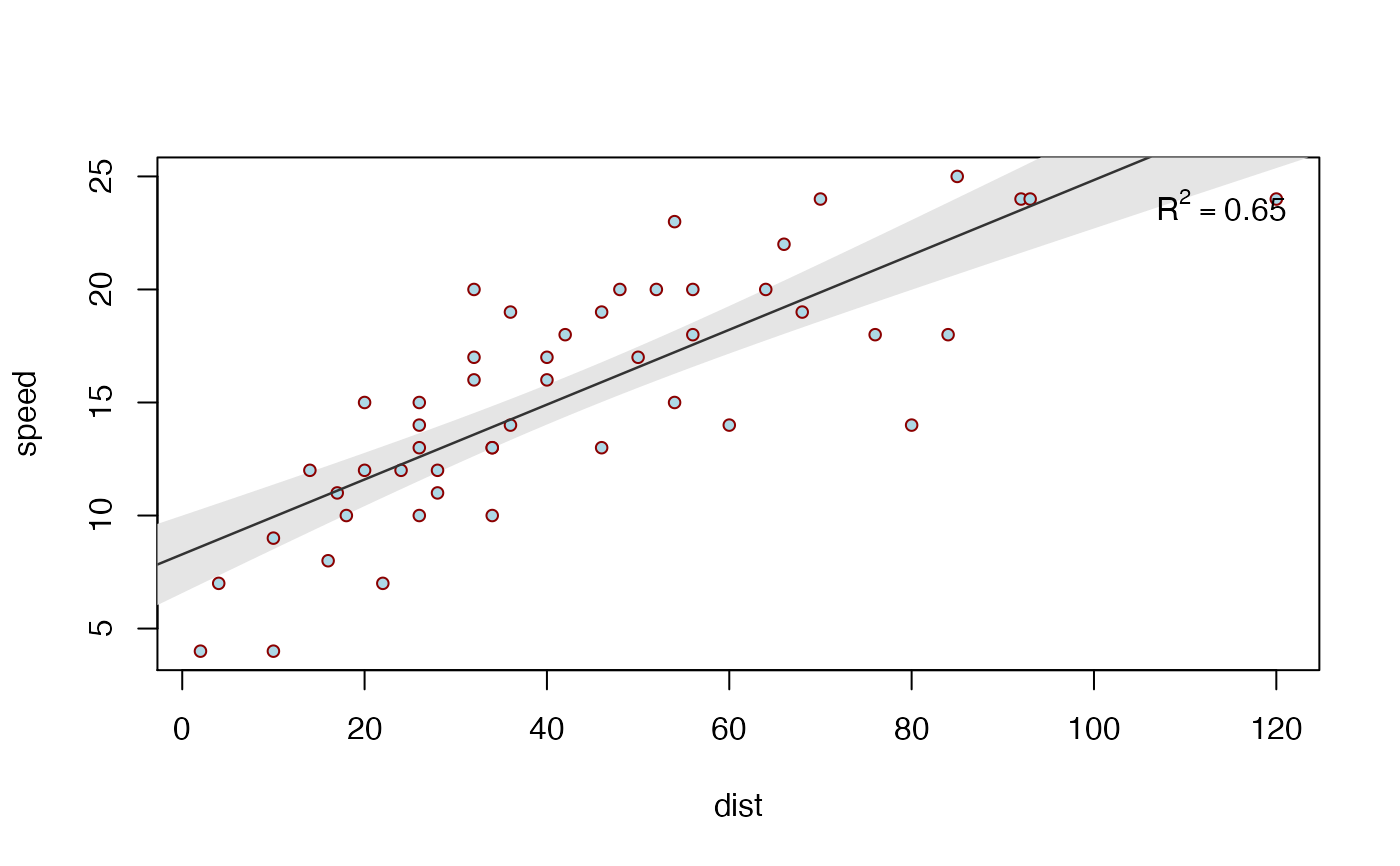
# Linear regression
biVarPlot(data = cars, x = dist, y = speed)
 #>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -7.5293 -2.1550 0.3615 2.4377 6.4179
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.28391 0.87438 9.474 1.44e-12 ***
#> iv 0.16557 0.01749 9.464 1.49e-12 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 3.156 on 48 degrees of freedom
#> Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
#> F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
#>
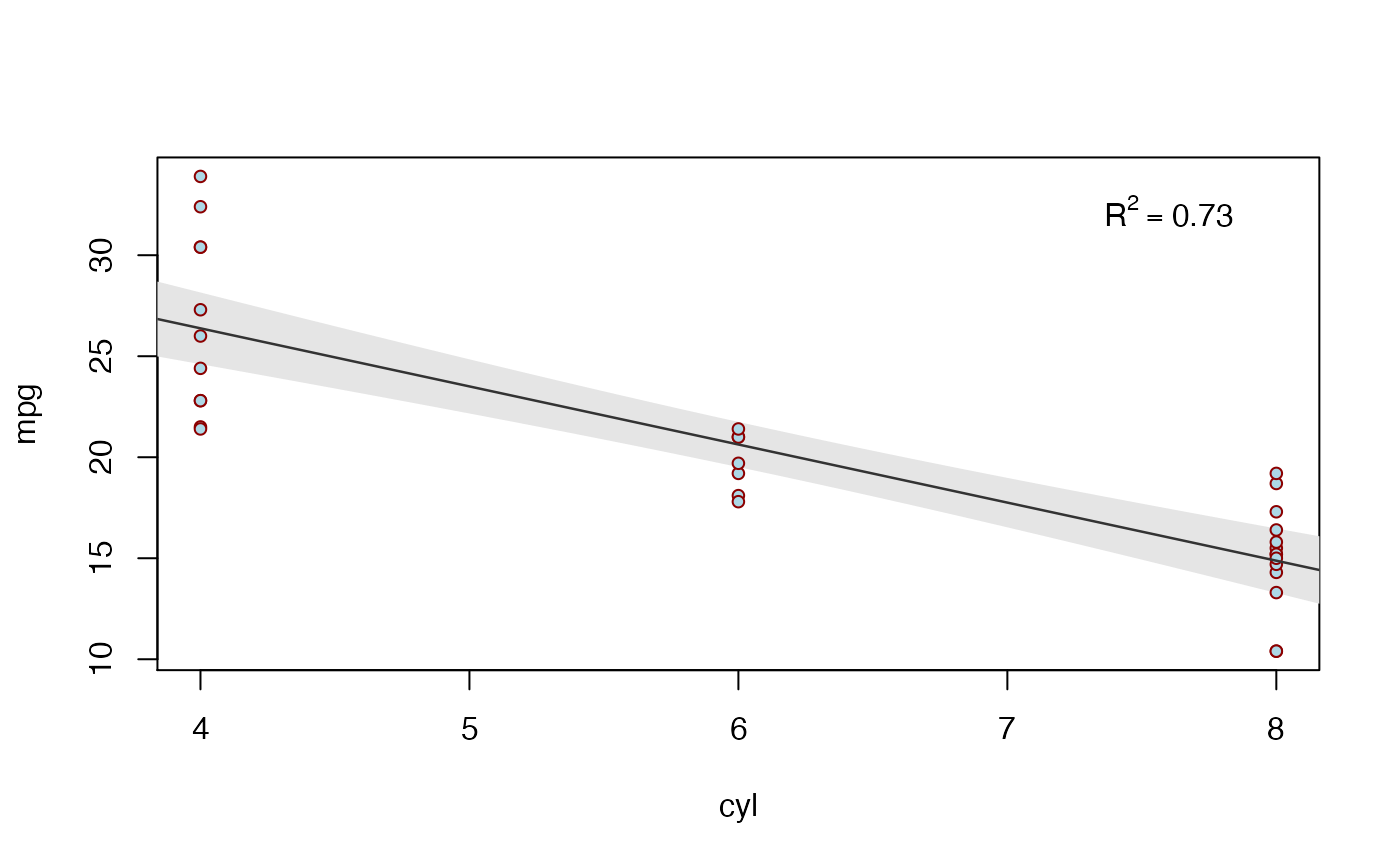
biVarPlot(data = mtcars, x = cyl, y = mpg)
#>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -7.5293 -2.1550 0.3615 2.4377 6.4179
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.28391 0.87438 9.474 1.44e-12 ***
#> iv 0.16557 0.01749 9.464 1.49e-12 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 3.156 on 48 degrees of freedom
#> Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
#> F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
#>
biVarPlot(data = mtcars, x = cyl, y = mpg)
 #>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.9814 -2.1185 0.2217 1.0717 7.5186
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 37.8846 2.0738 18.27 < 2e-16 ***
#> iv -2.8758 0.3224 -8.92 6.11e-10 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 3.206 on 30 degrees of freedom
#> Multiple R-squared: 0.7262, Adjusted R-squared: 0.7171
#> F-statistic: 79.56 on 1 and 30 DF, p-value: 6.113e-10
#>
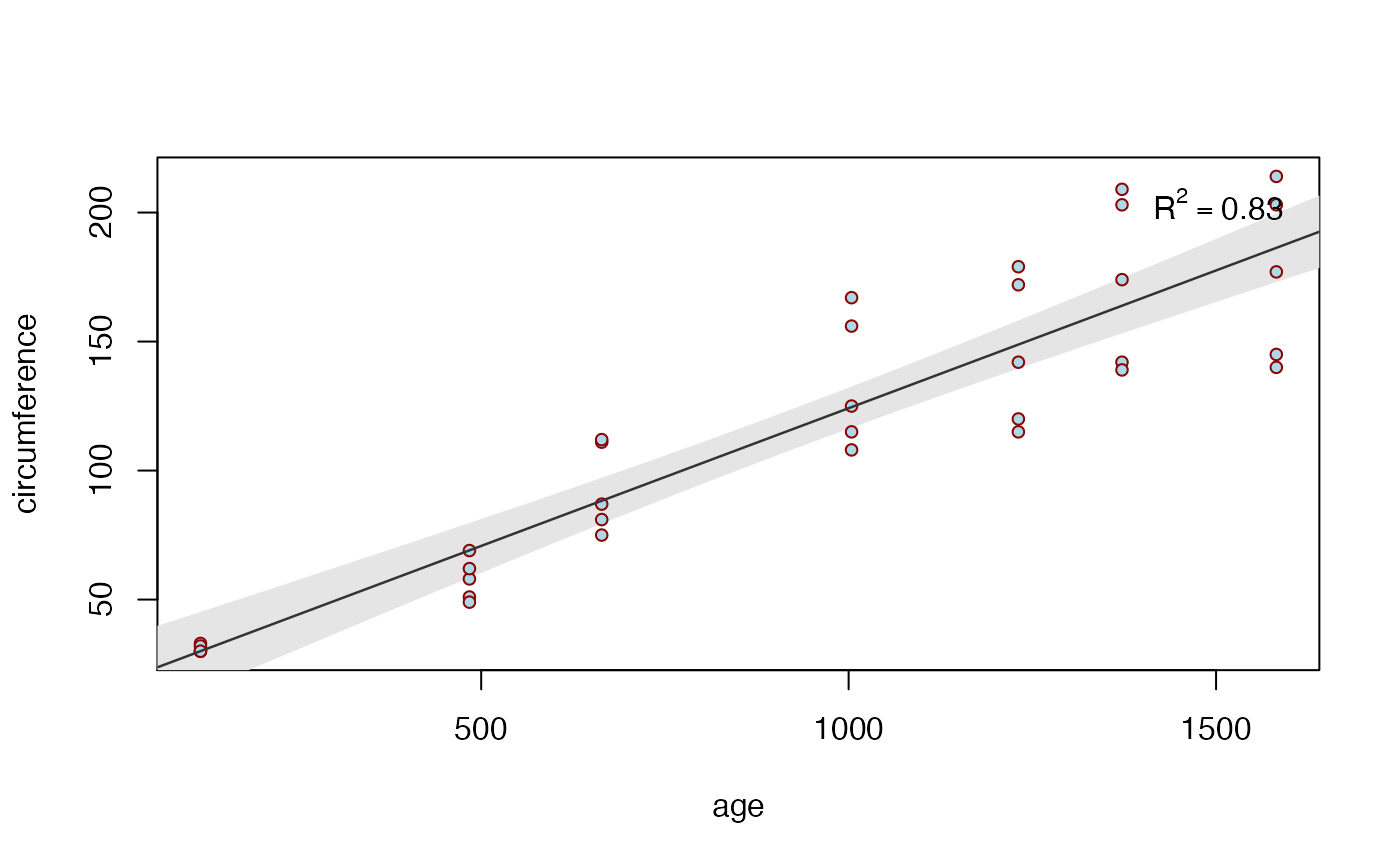
biVarPlot(data = Orange, x = age, y = circumference)
#>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.9814 -2.1185 0.2217 1.0717 7.5186
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 37.8846 2.0738 18.27 < 2e-16 ***
#> iv -2.8758 0.3224 -8.92 6.11e-10 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 3.206 on 30 degrees of freedom
#> Multiple R-squared: 0.7262, Adjusted R-squared: 0.7171
#> F-statistic: 79.56 on 1 and 30 DF, p-value: 6.113e-10
#>
biVarPlot(data = Orange, x = age, y = circumference)
 #>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -46.310 -14.946 -0.076 19.697 45.111
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.399650 8.622660 2.018 0.0518 .
#> iv 0.106770 0.008277 12.900 1.93e-14 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 23.74 on 33 degrees of freedom
#> Multiple R-squared: 0.8345, Adjusted R-squared: 0.8295
#> F-statistic: 166.4 on 1 and 33 DF, p-value: 1.931e-14
#>
biVarPlot(data = ChickWeight, x = Time, y = weight)
#>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -46.310 -14.946 -0.076 19.697 45.111
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.399650 8.622660 2.018 0.0518 .
#> iv 0.106770 0.008277 12.900 1.93e-14 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 23.74 on 33 degrees of freedom
#> Multiple R-squared: 0.8345, Adjusted R-squared: 0.8295
#> F-statistic: 166.4 on 1 and 33 DF, p-value: 1.931e-14
#>
biVarPlot(data = ChickWeight, x = Time, y = weight)
 #>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -138.331 -14.536 0.926 13.533 160.669
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 27.4674 3.0365 9.046 <2e-16 ***
#> iv 8.8030 0.2397 36.725 <2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 38.91 on 576 degrees of freedom
#> Multiple R-squared: 0.7007, Adjusted R-squared: 0.7002
#> F-statistic: 1349 on 1 and 576 DF, p-value: < 2.2e-16
#>
biVarPlot(data = USArrests, x = UrbanPop, y = Rape)
#>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -138.331 -14.536 0.926 13.533 160.669
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 27.4674 3.0365 9.046 <2e-16 ***
#> iv 8.8030 0.2397 36.725 <2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 38.91 on 576 degrees of freedom
#> Multiple R-squared: 0.7007, Adjusted R-squared: 0.7002
#> F-statistic: 1349 on 1 and 576 DF, p-value: < 2.2e-16
#>
biVarPlot(data = USArrests, x = UrbanPop, y = Rape)
 #>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -18.644 -5.476 -1.216 5.885 27.937
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.78707 5.71128 0.663 0.510
#> iv 0.26617 0.08513 3.127 0.003 **
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 8.626 on 48 degrees of freedom
#> Multiple R-squared: 0.1692, Adjusted R-squared: 0.1519
#> F-statistic: 9.776 on 1 and 48 DF, p-value: 0.003001
#>
# Logistic regression
vot <- rnorm(20, 15, 5)
vot <- sort(vot)
phon <- c(0,1,0,0,0,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1)
df1 <- data.frame(vot, phon)
biVarPlot(data = df1, x = vot, y = phon, family = 'binomial')
#>
#> Call:
#> lm(formula = dv ~ iv)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -18.644 -5.476 -1.216 5.885 27.937
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.78707 5.71128 0.663 0.510
#> iv 0.26617 0.08513 3.127 0.003 **
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 8.626 on 48 degrees of freedom
#> Multiple R-squared: 0.1692, Adjusted R-squared: 0.1519
#> F-statistic: 9.776 on 1 and 48 DF, p-value: 0.003001
#>
# Logistic regression
vot <- rnorm(20, 15, 5)
vot <- sort(vot)
phon <- c(0,1,0,0,0,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1)
df1 <- data.frame(vot, phon)
biVarPlot(data = df1, x = vot, y = phon, family = 'binomial')
 #>
#> Call:
#> glm(formula = dv ~ iv, family = family)
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -4.1462 1.8927 -2.191 0.0285 *
#> iv 0.3391 0.1471 2.306 0.0211 *
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 27.526 on 19 degrees of freedom
#> Residual deviance: 18.343 on 18 degrees of freedom
#> AIC: 22.343
#>
#> Number of Fisher Scoring iterations: 5
#>
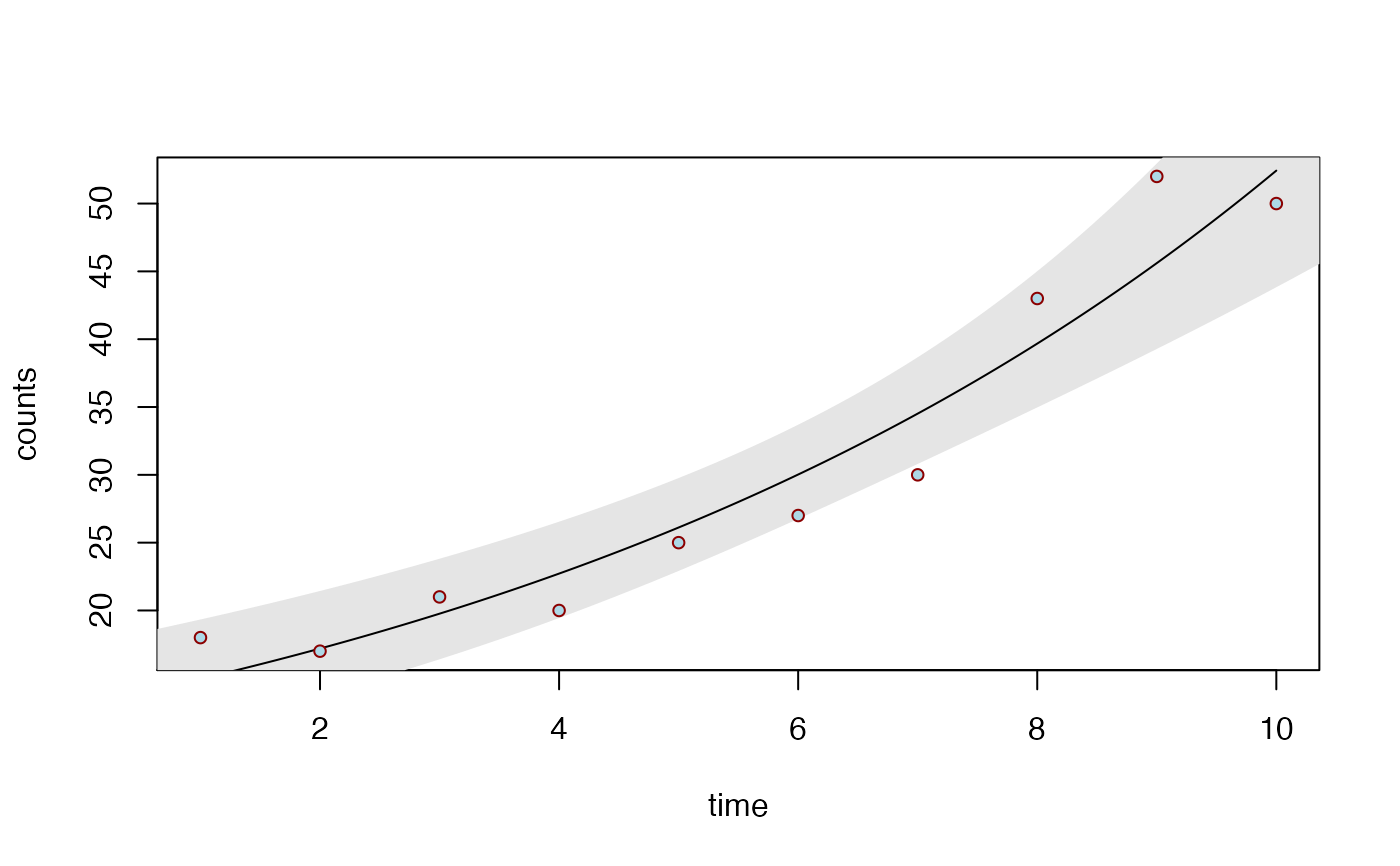
# Poisson regression
time <- 1:10
counts <- c(18, 17, 21, 20, 25, 27, 30, 43, 52, 50)
df2 <- data.frame(time, counts)
biVarPlot(data = df2, x = time, y = counts, family = 'poisson')
#>
#> Call:
#> glm(formula = dv ~ iv, family = family)
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -4.1462 1.8927 -2.191 0.0285 *
#> iv 0.3391 0.1471 2.306 0.0211 *
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 27.526 on 19 degrees of freedom
#> Residual deviance: 18.343 on 18 degrees of freedom
#> AIC: 22.343
#>
#> Number of Fisher Scoring iterations: 5
#>
# Poisson regression
time <- 1:10
counts <- c(18, 17, 21, 20, 25, 27, 30, 43, 52, 50)
df2 <- data.frame(time, counts)
biVarPlot(data = df2, x = time, y = counts, family = 'poisson')
 #>
#> Call:
#> glm(formula = dv ~ iv, family = "poisson")
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 2.56576 0.15017 17.086 < 2e-16 ***
#> iv 0.13937 0.02098 6.643 3.06e-11 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> (Dispersion parameter for poisson family taken to be 1)
#>
#> Null deviance: 49.5120 on 9 degrees of freedom
#> Residual deviance: 3.2222 on 8 degrees of freedom
#> AIC: 58.969
#>
#> Number of Fisher Scoring iterations: 4
#>
#>
#> Call:
#> glm(formula = dv ~ iv, family = "poisson")
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 2.56576 0.15017 17.086 < 2e-16 ***
#> iv 0.13937 0.02098 6.643 3.06e-11 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> (Dispersion parameter for poisson family taken to be 1)
#>
#> Null deviance: 49.5120 on 9 degrees of freedom
#> Residual deviance: 3.2222 on 8 degrees of freedom
#> AIC: 58.969
#>
#> Number of Fisher Scoring iterations: 4
#>